Stavros Komineas - Research

Magnetic vortices

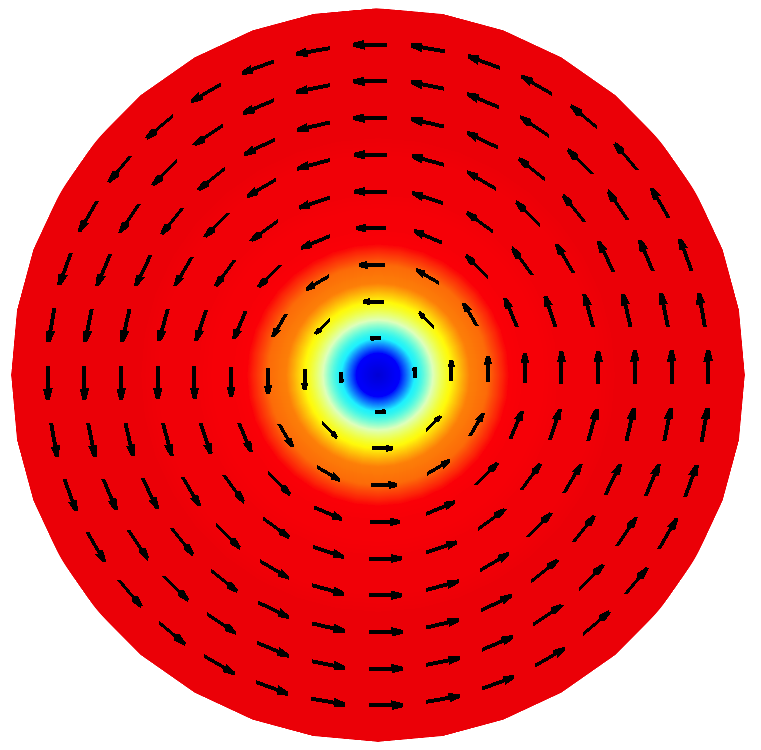
a magnetic vortex — A magnetic vortex. Shown is the projection of the magnetisation vector on the plane. The color encodes the third (out-of-plane) component of the magnetisation.

Magnetic vortices had been theoretically predicted early on but no experimental realisation had been achieved in ferromagnetic films, mainly because they have energy that diverges logarithmically with the sample size. The situation was suddenly reversed in the last two decades following the fabrication of mesoscopic ferromagnetic elements (< 1 μm). Since vortices were observed (in 2000) as stable and robust structures (indeed, as ground states) in mesoscopic magnetic elements, renewed interest was sparked and a very extensive experimental activity in academic and industrial laboratories has started.

Vortex-antivortex pairs

A vortex together with an antivortex form an interacting pair that is localized and has finite energy. A vortex-antivortex pair is thus, surprisingly, a more natural object from a physical and experimental point of view. We have studied theoretically the dynamics of vortex-antivortex dipoles, that is, a vortex together with an antivortex with opposite polarities. By exploiting a link between their topology and their dynamics we find that magnetic vortex-antivortex dipoles are in rotational motion, in stark contrast to vortex-antivortex pairs in fluid dynamics. [Phys. Rev. Lett. 2007].

When we include spin-transfer torque due to a spin-polarized current or the spin-Hall effect, we predict stable magnetization oscillations of the vortex-antivortex dipole due to a totally surprising cooperation of (conservative) Hamiltonian dynamics and of (non-conservative) spin torque forces [Europhys. Lett. 2012].

The vortex dipole acts as a microwave frequency generator at the nanoscale. Observations of such magnetisation oscillations, reported in [PRB 78, 174408 (2008)], had motivated our work.
The system gives interesting theoretical and mathematical results, e.g., the asymptotic analysis of a rotating vortex dipole [Physica D, 2015].
We propose vortex-antivortex pairs as advantageous structures which can, at the same time, be used as stable units for information storage (due to their topological structure) and also in logic operations (due to their dynamical behaviour) [Sci. Rep. 2015].

Presentation

A review on magnetic vortex-antivortex pairs.
Talk on "Rotating vortex-antivortex dipoles in ferromagnets under spin-polarised current", SIAM conference on Mathematical Aspects of Materials Science, Philadelphia, 10/6/2013.

Dynamics of point vortices

Trajectory of three point vortices in a bounded motion.

The equations of motion for point vortices in fluids were given by Helmholtz (1858) and by Kirchoff (1876) as a Hamiltonian system. We studied three point magnetic vortices using a method introduced by Gröbli in his seminal papers in 1877 [Vierteljahrsschrift 22/1, [Vierteljahrsschrift 22/2]. Magnetic vortices have a polarity and this is a feature not found in ordinary fluid vortices. We integrated completely the Hamiltonian system for magnetic vortices using conservation laws. [J. Math. Phys. 2010].

Remarks and Highlights

We demonstrate that some particular solutions describe the transmutation of linear momentum into vortex position. This counter-intuitive process is both physically relevant and mathematically rigorous. [New J. Phys. 2008].

Presentation

The motion of three magnetic point vortices on Wolfram Demonstrations.
"Groebli solution for magnetic vortices", NLQUGAS10, 13/4/2010, Ourense, Spain.