Δυναμική δινών
Εργαστηριακή άσκηση 4. (Παράδοση στο elearn) Μελετάμε και παραδίδουμε τις παρακάτω ασκήσεις (έχουν μόνο θεωρητικά ερωτήματα). Αγνοούμε τα ερωτήματα που αναφέρονται σε Λαγκρανζιανή (αυτό το θέμα θα το δούμε αργότερα).
- Μορφή εξισώσεων κίνησης.
- Κίνηση και ταχύτητα ζεύγους δινών.
- Τροχιές ζεύγους δινών από διατηρήσιμες ποσότητες.
Εργαστηριακή άσκηση 5. (Παράδοση στο elearn) Μελετάμε και παραδίδουμε τις παρακάτω ασκήσεις (έχουν θεωρητικά και αριθμητικά ερωτήματα).
- Τροχιές ζεύγους δινών.
- Δίνη σε εξωτερικό πεδίο.
Άσκηση (Μορφή εξισώσεων κίνησης). Αν V είναι το δυναμικό αλληλεπίδρασης μεταξύ δύο δινών, δείξτε ότι οι εξισώσεις κίνησης των δινών έχουν την μορφή \[ \gamma_1\dot{x}_1 = \frac{\partial V}{\partial y_1},\qquad \gamma_1\dot{y}_1 = -\frac{\partial V}{\partial x_1} \] με αντίστοιχες εξισώσεις για την δίνη 2, \[ \gamma_2\dot{x}_2 = \frac{\partial V}{\partial y_2},\qquad \gamma_2\dot{y}_2 = -\frac{\partial V}{\partial x_2}. \]
Το δυναμικό αλληλεπίδρασης είναι \[ V = - \gamma_1 \gamma_2 \ln |\boldsymbol{r}_1-\boldsymbol{r}_2|. \] Υπολογίζουμε τις ποσότητες \[ \frac{\partial V}{\partial x_1} = -\gamma_1\gamma_2 \frac{x_1-x_2}{|\boldsymbol{r}_1-\boldsymbol{r}_2|^2},\qquad \frac{\partial V}{\partial y_1} = \ldots\qquad \frac{\partial V}{\partial x_2} = \ldots\qquad \frac{\partial V}{\partial y_2} = \ldots \] Σημειώστε ότι μπορούμε να πάρουμε την εξίσωση για το $x_2$ εναλλάσοντας τους δείκτες 1 και 2 (στην πρώτη εξίσωση). Επίσης, μπορούμε να πάρουμε τις αντίστοιχες εξισώσεις για τα $y_1, y_2$ εναλλάσοντας τις μεταβλητές $x,y$. Συγκρίνουμε τα παραπάνω αποτελέσματα με τις εξισώσεις κίνησης (που έχουμε δει στις σημειώσεις του μαθήματος) και βρίσκουμε ότι \[ \gamma_1\dot{x}_1 = -\frac{\partial V}{\partial y_1},\qquad \gamma_2\dot{x}_2 = -\frac{\partial V}{\partial y_2},\qquad \gamma_1\dot{y}_1 = -\frac{\partial V}{\partial x_1},\qquad \gamma_2\dot{y}_2 = -\frac{\partial V}{\partial x_2}. \]Ερωτήσεις
- Θεωρήστε δυναμική V=V(r) και γράψτε τις εξισώσεις κίνησης. Ποιες είναι οι διατηρήσιμες ποσότητες για αυτή την περίπτωση;
Μαθησιακά αποτελέσματα
- Χαμιλτονιανή μορφή εξισώσεων.
Άσκηση (Κίνηση και ταχύτητα ζεύγους δινών). Θεωρείστε δύο δίνες με ισχύες (α) γ1=γ2 και (β) γ2=-γ1. Βρείτε την τροχιά που ακολουθούν και υπολογίστε την ταχύτητα κίνησης. [Υπόδειξη. Θα χρειαστεί να επαναλάβετε την διαδικασία που κάναμε στο μάθημα για αντίστοιχες απλούστερες περιπτώσεις.]
(α) Θέτουμε γ1=γ2=γ. Έχουμε τις διατηρήσιμες ποσότητες (με κατάλληλη επιλογή συστήματος συντεταγμένων) \[ \ell = |\boldsymbol{r}_1-\boldsymbol{r}_2|,\quad x_1 + x_2 = 0,\quad y_1 + y_2 = 0. \] Οι εξισώσεις για την δίνη 1 είναι \[ \dot{x}_1 = -\gamma\,\frac{y_1-y_2}{\ell^2} = -\frac{2\gamma}{\ell^2} y_1,\qquad \dot{y}_1 = \gamma\,\frac{x_1-x_2}{\ell^2} = \frac{2\gamma}{\ell^2} x_1. \] Συνδυάζοντας τις δύο εξισώσεις (δείξτε πώς), βρίσκουμε περιοδική κινηση με γωνιακή συχνότητα \[ \omega = \frac{2\gamma}{\ell^2}. \] Οι τροχιές είναι σε κύκλο ακτίνας $\ell$ (δείξτε το), άρα η γραμμική ταχύτητα της κάθε δίνης είναι \[ v = \omega \frac{\ell}{2} = \frac{\gamma}{\ell}. \] (β)Άσκηση (Τροχιές ζεύγους δινών από διατηρήσιμες ποσότητες). Θεωρείστε δύο δίνες με ισχύες γ1, γ2 με γ1 + γ2 ≠ 0. Βρείτε τις εξισώσεις για τις τροχιές τους χρησιμοποιώντας μόνο τις διατηρήσιμες ποσότητες Ix, Iy, E.
Υπόδειξη: Δείτε στο σύγγραμμα [ΚΧ].
Ερωτήσεις
- Συγκρίνετε το αποτέλεσμα με τα αριθμητικά αποτελέσματα (που θα βρείτε σε άλλη άσκηση).
Μαθησιακά αποτελέσματα
- Λύσεις ολοκληρώσιμου συστήματος.
Άσκηση (Τροχιές ζεύγους δινών).
Θεωρήστε δύο δίνες γ1, γ2 οι οποίες αλληλεπιδρούν με το δυναμικό
\[
V=-\gamma_1 \gamma_2\,\ln|\boldsymbol{r}_2-\boldsymbol{r}_1|.
\]
(α) Γράψτε την Λαγκρανζιανή και εξάγετε τις εξισώσεις κίνησης.
(β) Λύστε αριθμητικά τις εξισώσεις κίνησης και σχεδιάστε τις συντεταγμένες ως συναρτήσεις του χρόνου, $x_1(t), y_1(t), x_2(t), y_2(t)$,
(γ) Σχεδιάστε τις τροχιές των δινών στο επίπεδο xy.
(δ) Δείξτε (αριθμητικά) ότι οι διατηρήσιμες ποσότητες δεν μεταβάλλονται με τον χρόνο.
[Κάνετε τα παραπάνω για τις περιπτώσεις (i) γ1+γ2 ≠0 και (ii) γ1+γ2 = 0, για δική σας επιλογή των γ1, γ2].
(α) Η Λαγκρανζιανή είναι \[ L = \frac{\gamma_1}{2}\, (y_1 \dot{x}_1 - x_1 \dot{y}_1) + \frac{\gamma_2}{2}\, (y_2 \dot{x}_2 - x_2 \dot{y}_2) - V \] από την οποία εξάγουμε τις εξισώσεις κίνησης \[ \dot{x}_1 = -\gamma_2\,\frac{y_1-y_2}{|\boldsymbol{r}_1-\boldsymbol{r}_2|^2},\qquad \dot{x}_2 = -\gamma_1\,\frac{y_2-y_1}{|\boldsymbol{r}_1-\boldsymbol{r}_2|^2}, \] \[\dot{y}_1 = \gamma_2\,\frac{x_1-x_2}{|\boldsymbol{r}_1-\boldsymbol{r}_2|^2},\qquad \dot{y}_2 = \gamma_1\,\frac{x_2-x_1}{|\boldsymbol{r}_1-\boldsymbol{r}_2|^2}, \]
(β,γ)
Δείτε τον κώδικα python για 2 δίνες.
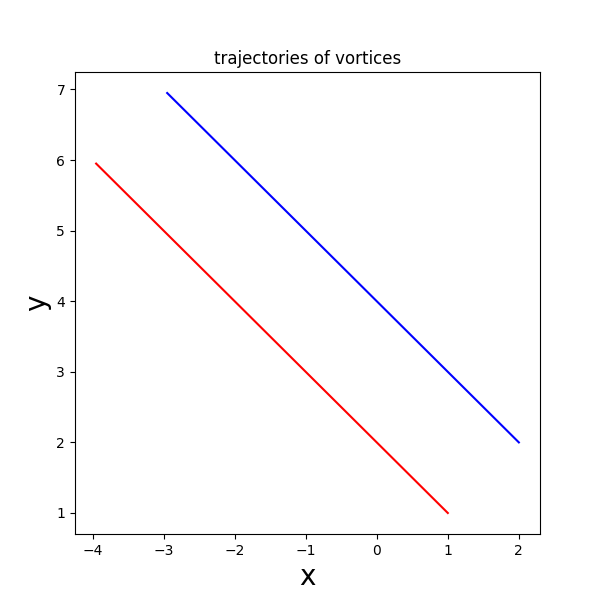
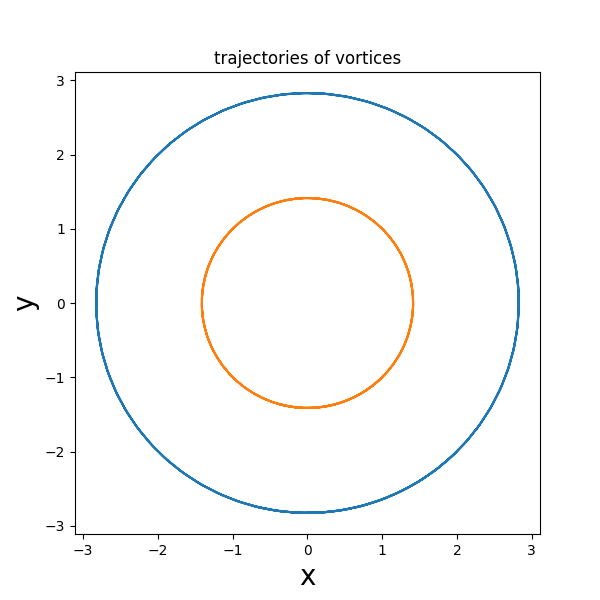
Δεξιά έχουμε τις τροχιές δύο δινών (με διαφορετικά χρώματα) στο επίπεδο xy.
Οι αρχική συνθήκη είναι (x1, y1)=(1,1), (x2, y2)=(2,2).
Στο σχήμα αριστερά έχουμε επιλέξει γ1=1, γ2=2.
Στο σχήμα δεξιά έχουμε επιλέξει γ1=1, γ2=-1.
(δ)
Ερωτήσεις
- Ποιες είναι οι τροχιές στην περίπτωση που η ολική ισχύς γ1+γ2 είναι πολύ μικρότερη του max(|γ1|, |γ2|);
Μαθησιακά αποτελέσματα
- Δυναμική και τροχιές μη-Νευτώνιων σωματίων.
- Συμπεριφορά ολοκληρώσιμων συστημάτων.
Άσκηση (Δίνη σε εξωτερικό πεδίο). (α) Γράψτε τη (γενική) Λαγκρανζιανή για μία δίνη γ σε εξωτερικό πεδίο το οποίο δίνεται από δυναμικό $V$. Δείξτε ότι οι εξισώσεις κίνησης είναι \[ \gamma\dot{x} = -\frac{\partial V}{\partial y},\qquad \gamma\dot{y} = \frac{\partial V}{\partial x}, \] (β) Θεωρήστε παραβολικό δυναμικό το οποίο να παγιδεύει τη δίνη και γράψτε την (ειδικότερη) Λαγκρανζιανή. (γ) Γράψτε και λύστε τις εξισώσεις κίνησης για το παραβολικό δυναμικό. (δ) Λύστε αριθμητικά τις εξισώσεις κίνησης για ένα άλλο δυναμικό (της επιλογής σας). Σχεδιάστε τροχιές της δίνης.
(α) Θεωρούμε $V=V(x,y)$. Η Λαγκρανζιανή είναι \[ L = \frac{\gamma}{2} (\dot{x}y - x\dot{y}) - V(x,y). \]
(β) Θεωρούμε παραβολικό δυναμικό \[ V(x,y) = \frac{k_1}{2} x^2 + \frac{k_2}{2} y^2. \] Bρίσκουμε τις εξισώσεις κίνησης \[ \gamma\dot{x} = k_2 y,\qquad \gamma\dot{y} = -k_1 x. \]
(γ) Για την μεταβλητή x έχουμε \[ \gamma\ddot{x} = k_2 \dot{y} \Rightarrow \ddot{x} + \frac{k_1 k_2}{\gamma^2} x = 0. \] Λύσεις είναι \[ x(t) = x_0 \cos(\omega t + \phi_0),\qquad y(t) = -y_0 \sin(\omega t + \phi_0),\qquad \omega = \frac{\sqrt{k_1 k_2}}{\gamma}, \] όπου οι $x_0, y_0, \phi_0$ είναι σταθερές και για να ικανοποιούνται οι αρχικές πρωτοτάξιες εξισώσεις ισχύει \[ y_0 = x_0 \sqrt{\frac{k_1}{k_2}}. \]
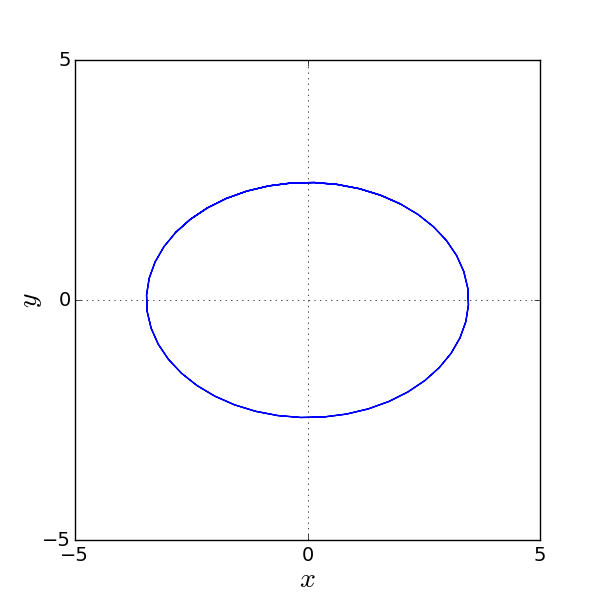
(δ) Δείτε τον κώδικα python ο οποίος λύνει το πρόβλημα αρχικών τιμών και σχεδιάζει την τροχιά της δίνης. Στο σχήμα έχουμε επιλέξει k1=1, k2=2. Βλέπουμε ότι η δίνη κάνει ελλειπτική τροχιά.
Ερωτήσεις
- Για το παραβολικό δυναμικό δείξτε ότι η δίνη κινείται επάνω σε ισοσταθμικές καμπύλες.
Μαθησιακά αποτελέσματα
- Χαμιλτονιανή περιγραφή των εξισώσεων κίνησης.
Άσκηση (Τροχιές N δινών). Θεωρήστε N δίνες γi οι οποίες αλληλεπιδρούν με το δυναμικό \[ V=-\gamma_i \gamma_j\,\sum_{i,j}\ln|\boldsymbol{r}_j-\boldsymbol{r}_i|. \] (α) Λύστε αριθμητικά τις εξισώσεις κίνησης και σχεδιάστε τις τροχιές των δινών στο επίπεδο xy. (β) Δείξτε (αριθμητικά) ότι οι διατηρήριμες ποσότητες δεν μεταβάλλονται με τον χρόνο.
(α) Δείτε έναν κώδικα python για N δίνες (και το αρχείο δεδομένων το οποίο διαβάζει).
Άσκηση (Κίνηση φορτίου σε δυναμικό). Θεωρήστε ένα φορτίο q υπό την επίδραση ομογενού μαγνητικού πεδίου $\mathbf{B}=(0,0,B)$ σε δυναμικό V(x,y). (α) Γράψτε τις εξισώσεις κίνησης. (β) Εξάγεται τις εξισώσεις για τον οδηγό κίνησης (guiding center). (γ) Γράψτε κώδικα ο οποίος να λύνει αριθμητικά το σύστημα των εξισώσεων. (δ) Θεωρήστε ένα παραβολικό δυναμικό και μελετήστε αναλυτικές λύσεις, επίσης (ε) λύστε αριθμητικά τις εξισώσεις.