Διαμερισματικά Μοντέλα και Διαστατική Ανάλυση

Εργαστηριακή άσκηση 1. (Παράδοση στο elearn) Μελετάμε και παραδίδουμε τις εξής ασκήσεις.

• Χημική αντίδραση σε αντιδραστήρα.
• Μη-γραμμικό μοντέλο αντίδρασης.
• Μόλυνση λίμνης

Άσκηση (Χημική αντίδραση σε αντιδραστήρα). Θεωρούμε την χημική αντίδραση στην παράγραφο 1.2.1 του βιβλίου [ΚX]. (α) Επιλύστε το αδιάστατο ΠΑΤ \begin{equation} \frac{d}{d\tau} \tilde{C}(\tau) = 1- \tilde{C}(\tau) - \beta \tilde{C}(\tau),\qquad \tilde{C}(\tau=0)=0. \end{equation} (β) Δώστε τη λύση στις αρχικές μεταβλητές. (γ) Συγκρίνετε την αριθμητική και την αναλυτική λύση του προβλήματος (δώστε γραφική παράσταση). (δ) Συγκρίνετε γραφικά την λύση για μικρό $\beta$ (π.χ., $\beta=0.2$) με τη λύση που έχουμε βρει για την περίπτωση αμεληταίου $\beta$.

(α) Η εξίσωση είναι γραμμική και μπορεί να γραφεί με απλούστερο τρόπο ως \begin{equation} \frac{d}{d\tau} \tilde{C}(\tau) = 1 - (1 + \beta) \tilde{C}(\tau). \end{equation} Έχει λύση εκθετική συνάρτηση της μορφής $\tilde{C}(\tau)=A + B e^{-\alpha \tau}$. Οι σταθερές $A=1/(1+\beta)$ και $\alpha=1+\beta$ υπολογίζονται ώστε η εκθετική μορφή να ικανοποιεί την διαφορική εξίσωση. Η σταθερά $B=-1/(1+\beta)$ υπολογίζεται ώστε να ικανοποιείται η αρχική συνθήκη $\tilde{C}(\tau=0)=0$. Η λύση είναι \begin{equation} \label{eq:linearSolution} \tilde{C}(\tau)= \frac{1}{1+\beta} \left(1 - e^{-(1+\beta) \tau} \right). \end{equation}

(β) Η αδιάστατη μορφή της εξίσωσης έχει προκύψει από τις αλλαγές μεταβλητών $\tilde{C} = C/C_{\rm εισ},\; \tau = \lambda t$ και τον ορισμό $\beta=k/\lambda$. Άρα, η λύση στις μεταβλητές $C, t$ είναι \begin{equation} C(t) = \frac{\lambda}{k+\lambda}\,C_{\rm εισ} \left(1 - e^{-(k+\lambda) t} \right). \end{equation}

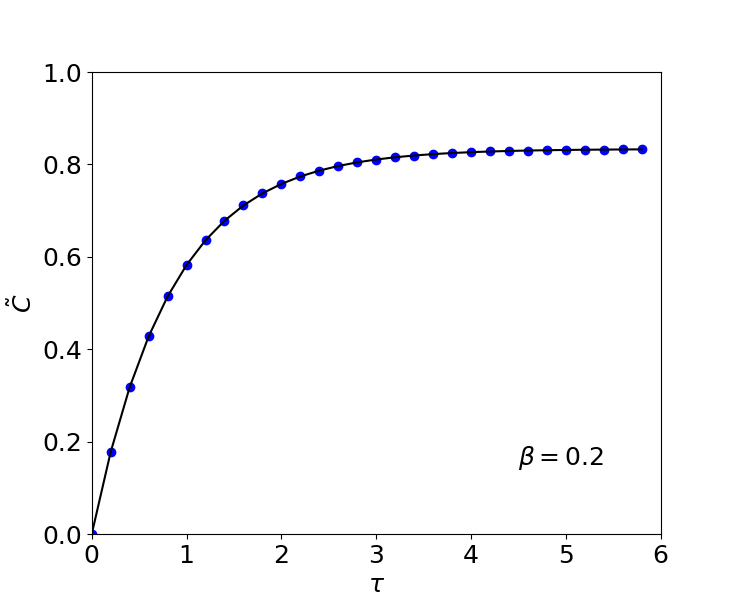
(γ) Το σχήμα δείχνει την εξέλιξη της συγκέντρωσης αντιδρώντος σε μία χημική αντίδραση. Η συνεχής μαύρη γραμμή δίνει την αναλυτική λύση (3) για $\beta=0.2$. Οι μπλε κύκλοι δείχνουν το αποτέλεσμα της αριθμητικής λύσης από τον κώδικα. Βλέπουμε ότι η αριθμητική λύση είναι μία εξαιρετική προσέγγιση της αναλυτικής λύσης.

Η αριθμητική λύση της διαφορικής εξίσωσης και η γραφική παράσταση έγιναν με κώδικα python (έναν λίγο απλούστερο κώδικα μπορείτε να δείτε εδώ).

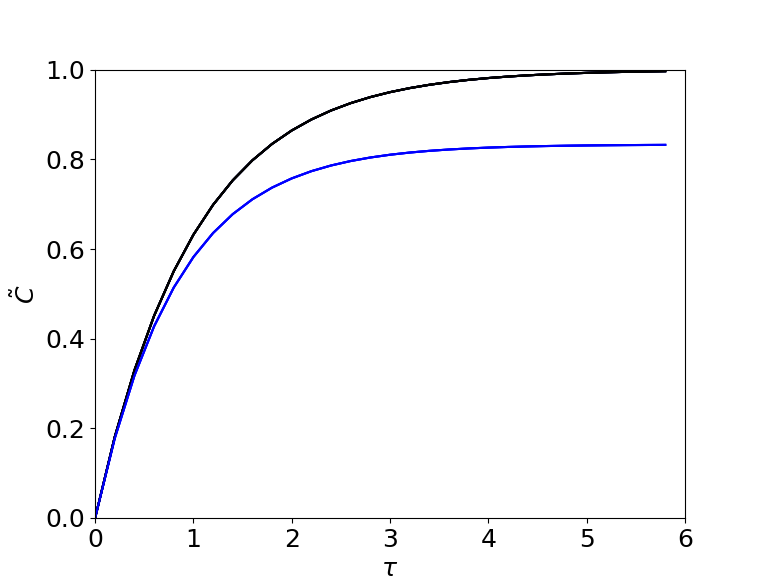
(δ) Η λύση για αμεληταίο $\beta$ είναι $\tilde{C}(\tau)= 1 - e^{-\tau}$ και η λύση για οποιοδήποτε $\beta$ δίνεται παραπάνω στην Εξ. (3). Βλέπουμε ότι για μεγάλους χρόνους η συγκέντρωση για $\beta=0$ είναι $\tilde{C}(\tau\to\infty) = 1$ (μαύρη γραμμή στο σχήμα), ενώ η συγκέντρωση για $\beta=0.2$ είναι $\tilde{C}(\tau\to\infty) = 1/1.2=0.83$ (μπλε γραμμή στο σχήμα).

Οι γραφικές παραστάσεις έγιναν με αυτόν τον κώδικα python.

Ερωτήσεις

• Δείτε ποια είναι η επίδραση στα χαρακτηριαστικά των λύσεων όταν αυξάνουμε το $\beta$.

Μαθησιακά αποτελέσματα

• Μοντελοποίηση διαδικασίας ισοζυγίου μάζας.
• Αριθμητική λύση διαφορικής εξίσωσης με έτοιμο πακέτο.
• Γραφικές παραστάσεις με υπολογιστή.
• Σύγκριση αριθμητικών και αναλυτικών λύσεων.

Άσκηση (Μη-γραμμικό μοντέλο αντίδρασης). Θεωρείστε τη χημική αντίδραση που είδαμε στην παράγραφο 1.2.1 του [ΚΧ]. Υποθέστε ότι ο ρυθμός αντίδρασης είναι μη-γραμμικός, της μορφής \begin{equation} \label{eq:nonlinearRate} \rho(C) = k C^2. \end{equation} (α) Γράψτε το μοντέλο για την συγκέντρωση του αντιδρώντος. (β) Γράψτε την αδιάστατη μορφή του μοντέλου. (γ) Βρείτε αριθμητικά λύσεις για την συγκέντρωση $C=C(t)$ και συγκρίνετε τις λύσεις με αυτές που προέκυψαν στο γραμμικό μοντέλο, π.χ., στην προηγούμενη άσκηση. (δ) Ποια είναι η σταθερή κατάσταση στην οποία φθάνει η αντίδραση (για μεγάλους χρόνους);

(α) Η γενική εξίσωση για την χημική αυτή αντίδραση είναι \[ \frac{d}{dt} C(t) = \lambda C_{\rm εισ} - \lambda C(t) - \rho(C(t)). \] Εδώ αντικαθιστούμε τον δεδομένο μη-γραμμικό ρυθμό αντίδρασης \eqref{eq:nonlinearRate} και έχουμε τo μοντέλο \begin{equation} \label{eq:nonlinearModel0} \frac{d}{dt} C(t) = \lambda C_{\rm εισ} - \lambda C - k C^2. \end{equation}

(β) Για να κάνουμε αδιαστατοποίηση συγκρίνουμε μεταξύ τους τους όρους της Εξ. \eqref{eq:nonlinearModel0} για να βρούμε κατάλληλες νέες μεταβλητές. Συγκρίνοντας τον όρο στο αριστερό μέλος (την παράγωγο) με τον 1ο ή 2ο όρο στο δεξιό μέλος βλέπουμε ότι το $\lambda$ παριστάνει αντίστροφο χρόνο. Ώστε μπορούμε να ορίσουμε την αδιάστατη χρονική μεταβλητή $\tau=\lambda t$. Επίσης ορίζουμε $\tilde{C}=C/C_{\rm εισ}$. Με αντικατάσταση στην Εξ. \eqref{eq:nonlinearModel0} έχουμε \begin{equation} \label{eq:nonlinearModel} \frac{d}{d\tau} \tilde{C}(\tau) = 1 - \tilde{C} - \beta\tilde{C}^2,\qquad \beta= \frac{k C_{\rm εισ}}{\lambda}. \end{equation} Η εξίσωση είναι μη-γραμμική. Η αδιάστατη παράμετρος $\beta$ εξαρτάται όχι μόνο από τον ρυθμό παροχής $\lambda$ και την παράμετρο για τον ρυθμό κατανάλωσης $k$ (όπως στην προηγούμενη άσκηση), αλλά και από την συγκέντρωση παροχής $C_{\rm εισ}$.

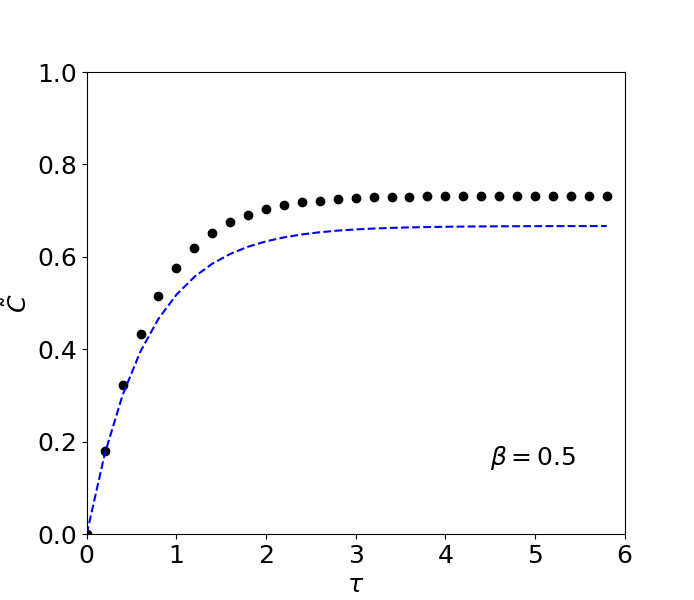
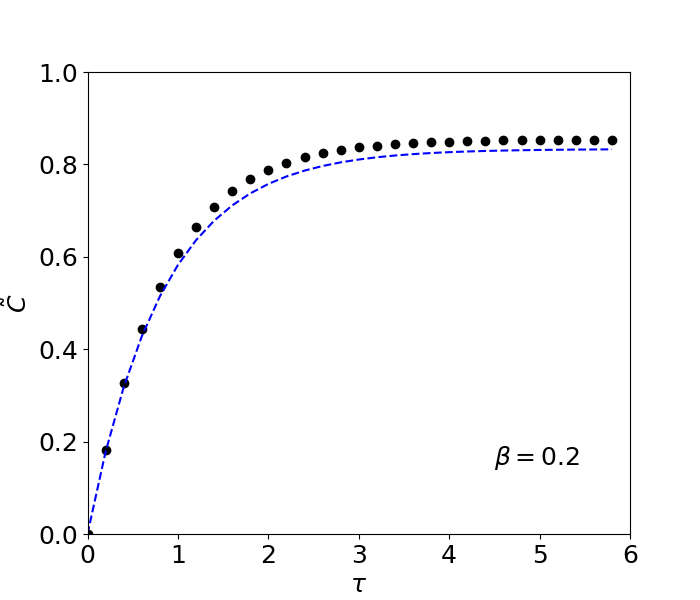
(γ) Λύνουμε την μη γραμμική διαφορική εξίσωση με έναν κώδικα python. Για να κάνουμε σύγκριση με το γραμμικό μοντέλο χρησιμοποιούμε την λύση \eqref{eq:linearSolution}. Η λύση για μικρό $\beta$ (μαύροι κύκλοι) είναι κοντά στην λύση του γραμμικού μοντέλου για το ίδιο $\beta$ (μπλε διακεκομμένη γραμμή). Για μεγαλύτερες τιμές του $\beta$ (π.χ., για $\beta=0.5$) οι λύσεις του γραμμικού και του μη-γραμμικού μοντέλου αποκλίνουν περισσότερο.

(δ) Για μεγάλους χρόνους, η συγκέντρωση υπολογίζεται αν θέσουμε $d\tilde{C}/d\tau=0$ στην Εξ. \eqref{eq:nonlinearModel}. Έχουμε την εξίσωση $1 - \tilde{C} - \beta\tilde{C}^2 = 0$ και την λύση \[ \tilde{C}(\tau\to\infty) = \frac{-1+\sqrt{1+4\beta}}{2\beta}. \]

Ερωτήσεις

• Σε ποια περίπτωση η διαδικασία της μη-γραμμικής αντίδρασης είναι παρόμοια και σε ποια είναι αρκετά διαφορετική από την γραμμική αντίδραση;
• Πώς σχετίζεται η λύση για μεγάλους χρόνους του μη-γραμμικού μοντέλου με εκείνην του γραμμικού μοντέλου;

Μαθησιακά αποτελέσματα

• Παραγωγή μη-γραμμικού μοντέλου.
• Αριθμητική λύση μη-γραμμικής διαφορικής εξίσωσης με έτοιμο πακέτο.

Άσκηση (Μόλυνση λίμνης). Σε μία λίμνη όγκου $V$ (σε $m^3$) ρέει μολυσμένο νερό από έναν ποταμό με ρυθμό $F$ (σε $m^3/h$). Το εισρεόμενο νερό περιέχει μολυσμένη ουσία πυκνότητας $\rho_{\rm in}$ (σε $kg/m^3$). Το νερό εκρέει από την λίμνη με τον ίδιο ρυθμό $F$. (α) Εξάγετε ένα μοντέλο για την πυκνότητα μολυσμένης ουσίας στο νερό της λίμνης. (β) Ποια η πυκνότητα μολυσμένης ουσίας στην λίμνη μετά από πολύ χρόνο;
Ας υποθέσουμε τώρα ότι ο Δήμος εγκαθιστά ένα σύστημα καθαρισμού το οποίο μπορεί να καθαρίζει το νερό της λίμνης με ρυθμό $R$ (σε $kg/h$) δηλαδή μπορεί να αφαιρεί μάζα $R$ μολυσμένης ουσίας ανά ώρα. (γ) Γράψτε ένα μοντέλο το οποίο να περιλαμβάνει αυτή την διαδικασία. (δ) Ποια η πυκνότητα μολυσμένης ουσίας στην λίμνη μετά από πολύ χρόνο (εφόσον λειτουργεί συνεχώς το σύστημα καθαρισμού);

(α) Θεωρούμε $\rho$ την πυκνότητα μολυσμένης ουσίας στην λίμνη. Κάνουμε την απλοποιητική παραδοχή είναι η $\rho$ είναι ομοιόμορφη σε όλη την λίμνη. Η μάζα μολυσμένης ουσίας στην λίμνη είναι $m=\rho V$. Η διατήρηση της μάζας εκφράζεται ως εξής \[ V\frac{d\rho}{dt} = \rho_{\rm in} F - \rho F. \] Δηλαδή, η διαφορά της εξερχόμενης από την εισερχόμενη μάζα (μολυσμένης ουσίας) είναι ίση με την μεταβολή της μάζας εντός της λίμνης. Η εξίσωση γράφεται και ως \[ \frac{d\rho}{dt} = \frac{F}{V} (\rho_{\rm in} - \rho). \]

(β) Αν υποθέσουμε ότι αρχικά δεν υπήρχε μολυσμένη ουσία στην λίμνη, $\rho(t=0)=0$, τότε το δεξιό μέλος της εξίσωσης ειναι θετικό. Το $\rho$ θα αυξηθεί και, όταν το δεξιό μέλος γίνει μηδέν, θα έχουμε μία σταθερή πυκνότητα (για μεγάλο χρόνο). Αυτή θα είναι \[ \rho_{\rm in} F - \rho F \Rightarrow \rho = \rho_{\rm in}. \]

(γ) Η διατήρηση της μάζας εκφράζεται ως εξής \[ V\frac{d\rho}{dt} = \rho_{\rm in} F - R - \rho F \] ή \[ \frac{d\rho}{dt} = \frac{F}{V} \left( \rho_{\rm in} - \frac{R}{F} - \rho \right). \]

(δ) Θα έχουμε μία σταθερή πυκνότητα (για μεγάλο χρόνο) όταν \[ \rho_{\rm in} F - R - \rho F \Rightarrow \rho = \rho_{\rm in} - \frac{R}{F}. \]

Ερωτήσεις

• Ποιες είναι οι ομοιότητες στην κατασκευή του μοντέλου με εκείνο για την χημική αντίδραση;

Μαθησιακά αποτελέσματα

• Εξαγωγή διαμερισματικού μοντέλου.

Άσκηση (Μετάπτωση μαγνητικής ροπής). Η εξίσωση κίνησης του διανύσματος της μαγνητικής ροπής $\boldsymbol{\mu}$ ενός ατόμου το οποίο βρίσκεται μέσα σε μαγνητικό πεδίο $\boldsymbol{B}$ είναι \begin{equation} \label{eq:momentDynamics0} \frac{d\boldsymbol{\mu}}{dt} = \gamma\, \boldsymbol{\mu}\times\boldsymbol{B} \end{equation} όπου $\gamma$ είναι μία φυσική σταθερά η οποία λέγεται γυρομαγνητικός λόγος. Μία τυπική τιμή του μέτρου μαγνητικής ροπής ατόμου είναι η σταθερά $\mu_B$ η οποία λέγεται μαγνητόνη του Bohr. (α) Δείξτε ότι το διάνυσμα της μαγνητικής ροπής δεν μεταβάλλει το μέτρο του κατά την κίνηση σε μαγνητικό πεδίο. (β) Ορίστε νέες μεταβλητές και δώστε μία αδιάστατη μορφή της εξίσωσης (θεωρήστε $|\boldsymbol{\mu}|=\mu_B$ και ένα σταθερό μαγνητικό πεδίο, έστω $\boldsymbol{B}=B\,\boldsymbol{z}$). (γ) Δώστε τη γενική λύση της διανυσματικής αυτής εξίσωσης στις αδιάστατες μεταβλητές. (δ) Μετατρέψτε τη λύση στις αρχικές (φυσικές) μεταβλητές.

(α) Θα υπολογίσουμε την χρονική μεταβολή του μέτρου του $\boldsymbol{\mu}$ με την βοήθεια της εξίσωσης κίνησής του \eqref{eq:momentDynamics0}. Είναι απλούστερο να πάρουμε την χρονική μεταβολή του τετραγώνου του μέτρου: \[ \frac{d}{dt} |\boldsymbol{\mu}|^2 = \frac{d}{dt} (\boldsymbol{\mu}\cdot\boldsymbol{\mu}) = 2\,\boldsymbol{\mu}\cdot \frac{d \boldsymbol{\mu}}{dt} = 2\gamma\,\boldsymbol{\mu}\cdot (\boldsymbol{\mu}\times \boldsymbol{B}) = 0. \] Το τελικό αποτέλεσμα είναι μηδέν διότι το $\boldsymbol{\mu}$ εμφανίζεται δύο φορές στο μικτό γινόμενο.

(β) Η εξίσωση είναι γραμμική στο $\boldsymbol{\mu}$ ώστε μπορούμε να το κανονικοποιήσουμε με όποια ποσότητα θέλουμε. Είναι φυσιολογικό να κανονικοποιήσουμε το $\boldsymbol{\mu}$ με το $\mu_B$, ...

(γ) Αν πάρουμε τις συνιστώσες του διανύσματος $\boldsymbol{m} = (m_1,m_2,m_3)$ η διανυσματική εξίσωση γράφεται ως \begin{equation} \label{eq:momentDynamicsComponents} \frac{d m_1}{d\tau} = m_2,\quad \frac{d m_2}{d\tau} = -m_1,\quad \frac{d m_3}{d\tau} = 0. \end{equation} Η τελευταία εξίσωση λύνεται αμέσως και μας λέει ότι $m_3={\rm const.}$, δηλαδή ότι η συνιστώσα του $\boldsymbol{m}$ στην κατεύθυνση του $\boldsymbol{B}$ παραμένει σταθερή στον χρόνο. ...

(δ)

Ερωτήσεις

• Πώς μπορεί η απάντηση στο ερώτημα (α) να μας οδηγήσει στην κατανόηση της λύσης του προβλήματος;
• Πώς μπορούμε να εξάγουμε την τυπική συχνότητα του συστήματος χωρίς να βρούμε την πλήρη λύση της εξίσωσης;

Μαθησιακά αποτελέσματα

• Κατανόηση μοντέλου με διανυσματική μεταβλητή.
• Μέθοδος λύσης γραμμικής διαφορικής εξίσωσης 2ης τάξης.